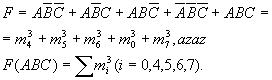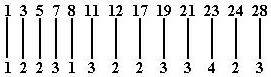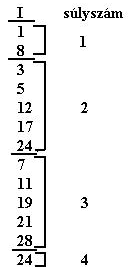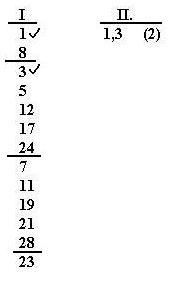(Quine – Mc Cluskey módszer)

 

A következő példa feldolgozása előtt fel kell még idéznünk a későbbiek megértése érdekében egy ritkábban használt azonosságot:

A(A+B)=A

Melynek segítségével gyorsan egyszerűsíthetők a következő alakú függvények:

A(A+B)(A+B+D)(B+D)D(B+C)=AD(B+C)=ABD+ACD

A Quine – Mc Cluskey módszer a logikai függvényben szereplő mintermek sorszámaiból indul ki, ezért a lehetséges felírási megoldások közül a következőt alkalmazzuk:

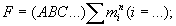
ahol n a változók száma, i a függvényben szereplő mintermek sorszáma. Ha a függvényt más alakban adták meg, első lépésként erre az alakra kell hozni:

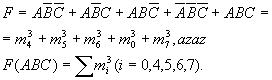Így már rendelkezésre állnak a minterm sorszámok, elkezdhető az egyszerűsítés.

A következőkben egy gyakorlati példán keresztül fogjuk bemutatni a Quine – Mc Cluskey eljárás menetét, főbb lépéseit.

Feladat:

Egyszerűsítsük a minterm sorszámok alapján az F függvényt!

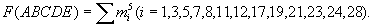
Az első lépés: felírjuk a súlyszámokat, azaz azt, hogy az egyes minterm sorszámok kettes számrendszerbeli alakjában hány darab 1-es van:

 

 
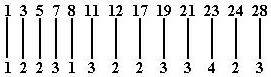
Az I. oszlop lényegében a minterm sorszámok csoportosított felsorolása. A kisebb súlyszámtól haladva a nagyobb felé, felsoroljuk az azonos súlyszámú minterm sorszámokat – egy-egy súlyszám csoporton belül növekvő sorrendben:

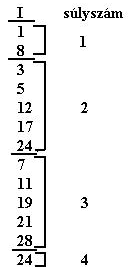  A továbbiakban a magyarázó feliratok természetesen feleslegesek a gyakorlatban az I. oszlop csak a sorszámokból áll. Az első oszlopban a mintermek önállóan szerepelnek, a II. oszlopban párosával – itt a kettes összevonási lehetőségeket tüntetjük fel.

A II. oszlop képzési szabályai a következők:

Az I. oszlopban mindig két, egymás alatt lévő csoportot hasonlítunk össze;

Az összehasonlítás során a kisebb súlyszámú csoport minden tagját a nagyobb súlyszámú csoport minden elemével össze kell vetni;

Ha az összehasonlított minterm sorszám összevonható páros, a két sorszámot a II. oszlopban a következő helyen egymás mellé írjuk, zárójelben feltüntetjük a különbségüket is (az összevonási számot), az I. oszlopban az összevont minterm sorszámokat – ha még nem volt pipájuk – kipipálással megjelöljük;

Az összevonhatóság feltételei:

1. a két csoport súlyszáma közötti különbség 1 legyen,
2. a minterm sorszámok különbsége (az összevonási szám) 2 egész kitevőjű hatvány legyen (azaz 1,2,4,8,16… stb.),
3. a nagyobb súlyszámú mintermsorszám számértéke is nagyobb legyen;
Nagyon fontos, hogy mindezeknek a feltételeknek egyidejűleg fenn kell állniuk!

Nézzen a felírt I. oszlop számsorára! A következő összehasonlításokat kell majd elvégeznünk:

1. az 1-et a 3-mal, 5-tel, 12-vel, 17-tel és 24-gyel,
2. a 8-at ugyanezekkel
kell összevetni, ekkor elkészült a II. oszlop első csoportja – a csoportokat a II. oszlopban is vízszintes vonal zárja le;
1. a 3-mat a 7-tl, a 11-gyel, a 19-cel, a 21-gyel, a 28-cal,
2. az 5-öt ugyanezekkel,
3. a 12-t ugyanezekkel,
4. a 17-t ugyanezekkel,
5. a 24-et ugyanezekkel
kell összehasonlítani, ekkor készült el a II. oszlop második csoportja;
1. a 7-et a 23-mal,
2. a 11-et a 23-mal,
3. a 19-et a 23-mal,
4. a 21-et a 23-mal,
5. a 28-at a 23-mal
vetjük össze, s ekkor készült el a II. oszlop utolsó csoportja.

Azért, hogy az összehasonlítási eljárást jól megérthesse, az első néhány lépést nagyon részletesen bemutatjuk – később már egy kicsit gyorsabban is haladhatunk. Az összehasonlításokat a fentebb rögzített sorrendben kell majd elvégeznünk.

Az első lépés: az 1 és a 3 összehasonlítása, ennek eredmény a következő: összevonhatóak, mivel a különbségük 2, és a nagyobb súlyszámú számértéke is nagyobb, azaz 3>1. A II. oszlopban tehát beírjuk az összevonható párost, zárójelben feltüntetve a különbségi számot: 1,3 (2); az egyes oszlopban pedig kipipáljuk az 1-es és 3-mas minterm sorszámokat (bár az 1 pipát kapott, tovább folytatjuk vele az összehasonlításokat, csak többször nem pipáljuk meg akkor sem, ha összevonhatónak találnánk!). Az eddigi eredményeink a következő ábrán láthatóak – az I. oszlop és a második oszlopból annak első eleme.



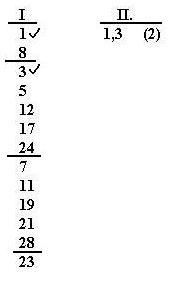
Az 1 és az 5 összehasonlítása is összevonhatóságot jelez, a sorszámok különbsége 4 (azaz 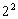), s a nagyobb súlyszám ismét nagyobb számértékű is (5>1). A II. oszlopban így felírható az összevonási pár és a különbségi szám: 1,5 (4) az I. oszlopban pipát kap az 5 sorszám is:



Az 1 és a 12 összehasonlítása eredménytelen – ezek nem vonhatóak össze, mivel különbségük nem 2 egész kitevőjű hatványa!
Az 1 és a 17 összehasonlítása ismét eredményes: ezek összevonhatóak, mivel különbségük16, azaz 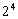és a nagyobb súlyszámú nagyobb számértékű is, 1,17 (16) jelzés kerül tehát a II. oszlopba, és a 17 is pipát kap az elsőben:
 



Az 1 és a 24 összehasonlítása nem hoz eredményt, a különbségük nem 2 egész kitevőjű hatványa.

Ezután a 8-at hasonlítjuk a második csoport elemeihez, az összevetések eredményeit kevésbé részletesen adjuk meg a következőkben:

1. a 8 a 3-mal hasonlítva: nem vonhatók össze, 3 < 8;
2. 8 az 5-tel hasonlítva: nem vonhatók össze, 5<8;
3. 8 a 12-vel hasonlítva: összevonhatóak, 8,12 (4);
4. 8 a 17-tel hasonlítva: nem vonhatók össze, a különbségük 9, nem kettő egész kitevőjű hatványa;
5. 8 a 24-el hasonlítva: összevonhatóak 8,24 (16). A most felfedezett összevonási lehetőségeket is beírva a II. oszlopba, annak első csoportja elkészült.
   
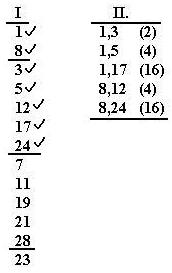
Most az első oszlopban a második csoportot a harmadikkal kell összehasonlítanunk, az összehasonlításra kerülő számpárok szintén szerepeltek már a korábbiakban, s az összehasonlítási sorrend is az ott rögzített sorrendnek felel meg.

Az összehasonlítások eredménylistája a következő:

• 3,7 (4) – összevonható;
• 3,11 (8) – összevonható;
• 3,19 (16) – összevonható;
• a 3,21 ill. a 3,28 nem összevonhatók;
• 5,7 (2) – összevonhatók;
• az 5,11 ill. az 5,19 nem vonhatók össze;
• 5,21 (16) - összevonható;
• az 5,28 a 12,7 a 12,11 a 12,19 a 12,21 nem vonhatók össze;
• 12,28 (16) – összevonhatók;
• a 17,7 és a 17,11 nem vonhatók össze;
• a 17,19 (2) – összevonhatók;
• 17,21 (4) – összevonhatók;
• a 17,28 nem vonhatók össze;
• a 24,7 a 24,11 a 24,19 a 24,21 nem vonhatók össze;
• a 24,28 (4) – összevonhatók.
    A II. oszlopban írjuk be az összevonható párosokat s az I-es oszlopokban pipáljuk meg az újonnan a II-es oszpoba került minterm sorszámokat:  

Végül az I. oszlop harmadik csoportja tagjait kell összehasonlítani a 23-mal:

• 7,23 (16) – összevonhatók;
• 11,23 – nem vonhatók össze;
• 19,23 (4) – összevonhatók;
• 21,23 (2) – összevonhatók;
• 28,23 – nem vonhatók össze. A II. oszlop most teljesen elkészült:


    Említettem már, hogy a II. oszlop lehetséges összes kettes összevonást tartalmazza, a III. oszlopban a négyes összevonások jelennek majd meg. A II. oszlopból most minterm párosokat hasonlítunk össze a következő csoport minterm párosaival – de az összevonhatósági szabálysor egy további feltétellel bővül:

• csak azonos összevonási minterm párosok vonhatóak össze négyes összevonássá!
    Mivel egy négyes összevonás kétféleképpen is kialakítható kettős összevonásokból, minden négyes összevonási lehetőséget kétszer kell megtalálnunk a II. oszlop elemei összehasonlítása során, de csak egyszer tüntetjük fel a III. oszlopban. A négyes összevonási lehetőségek első felfedezésekor a minterm sorszámok sorrendben követik egymást s az új összevonási szám nagyobb a réginél. Ekkor írjuk be a III. oszlopba. A második előforduláskor a minterm sorszámok kevert sorrendűek, s az új összevonási szám kisebb a réginél. Ekkor nem írjuk be a II. oszlopba de a II. oszlopban az esetleg esedékes pipákat bejelöljük ekkor is. Ha egy összevonási lehetőségnek nem találjuk meg mindkét változatát, vagy először a kevert sorrendű összevonási lehetőségre bukkanunk rá – célszerű az egész eddigi egyszerűsítési eljárást tüzetesen átnézni, mert valamit elrontottunk, valamit elnéztünk benne.

    A II. oszlop első és második csoportja összehasonlításának eredményeit sorolom fel az alábbiakban - de csak az azonos régi összevonási számúkat hasonlítjuk össze:

• 1,3 (2) az 5,7 (2) –vel összevonható: 1,3,5,7 (2,4)
• 1,3 (2) a 17,19 (2)-vel összevonható: 1,3,17,19 (2,16)
• 1,5 (4) a 3,7 (4)-gyel összevonható, de nem írjuk fel, mert szerepel már a III. oszlopban, csak a pipákat tesszük ki;
• 1,5 (4) a 17,21 (4)-gyel összevonható: 1,5,17,21 (4,16)
• 1,17 (16) a 3,19 (16)-tal összevonható, de már szerepel;
• 1,17 (16) a 5,21 (16)-tal összevonható, de már szerepel;
• 1,17 (16) és 12,28 (16) nem vonhatóak össze ugyanis a különbségük értéke 11;
• 8,12 (4) és 3,7 (4) nem vonhatók össze;
• 8,12 (4) és 17,21 (4) nem vonhatók össze mert különbségük 9;
• 8,12 (4) a 24,28 (4)-gyel összevonható: 8,12,24,28 (4,16);
• 8,24 (16) és 3,19 (16) nem vonható össze;
• 8,24 (16) és 5,21 (16) nem vonható össze;
• 8,24 (16) a 12,28 (16)-tal összevonható de már szerepel;
    Az eddigieket beírva a III. oszlopba, annak első csoportja el is készült. A második csoportjához a következő kiértékeléseket kell elvégezni:
• 3,7 (4) a 19,23 (4)-gyel összevonható: 3,7,19,23 (4,16);
• 3, 19 (16) és a 7,23 (16) összevonható, de már szerepel;
• 5,7 (2) a 21,23 (2)-vel összevonható: 5,7,21,23 (2,16);
• 5,21 (16) és a 7,23 (16) összevonható, de már szerepel;
• 12,28 (16) a 7,23 (16)-tal nem vonható össze;
• 17,19 (2) és a 21,23 (2) összevonható: 17,19,21,23 (2,4);
• 17,21 (4) a 19,23 (4)-gyel összevonható, de már szerepel;
• 24,28 (4) és a 19,23 (4) nem vonható össze;
Az összevonható négyeseket beírva, a III. oszlop is elkészült:

 

A III. oszlopból a IV.-et hasonló módon képezzük, minta a III.-at a II.-ból – de minden nyolcas összevonást háromszor kell megtalálnunk! Most is csak az első, sorrendben jelentkező nyolcas összevonást írjuk be a IV. oszlopba, a többi esetben csak pipákat rajzolunk be a III. oszlopba.

A III. oszlop elemei közötti összehasonlítások eredményei a következők (csak azokat az elemeket hasonlítjuk össze, melyeknél a régi különbségi számok azonosak):

• 1,3,5,7 (2,4) és 17,19,21,23 (2,4) összevonható: 1,3,5,7,17,19,21,23 (2,4,16);
• 1,3,17,19 (2,16) és 5,7,21,23 (2,16) összevonható, de már szerepel;
• 1,5,17,21 (4,16) és 3,7,19,23 (4,16) összevonható, de már szerepel;
• 8,12,24,28 (4,16) és 3,7,19,23 (4,16) nem vonható össze.
 

Az eredményeket felhasználva a IV. oszlop is felírható:

 

    A táblázat elkészült, nagyszámú eleme pipát kapott, de több olyan is szerepel benne, melyek nincsenek megjelölve pipával. A pipa azt jelenti, hogy az illető minterm vagy összevont minterm csoport nagyobb összevonási egységben is szerepel – a pipa nélküliek már nem szerepelnek nagyobb összevont egységekben. Ezek e pipa nélküli részletek a függvény felépítésére használható építő elemek – prím implikánsok. Jelöljük a prím implikánsokat az ABC első kisbetűivel!

 

Példánkban három prím implikáns adódott:

a 3,11 (8)

b 8,12,24,28 (4,16)

c 1,3,5,7,17,19,21,23 (2,4,16).

A függvények többségénél nem szükséges minden prím implikáns a függvény megvalósításához. Úgy kell kiválasztanunk a megvalósításra szánt prím implikánsokat, hogy azok a függvény minden mintermjét tartalmazzák – s a lehető legegyszerűbb alakot szolgáltassák, azaz a lehető legkevesebb prím implikánst kelljen felhasználni. A szükséges prím implikánsok kiválasztását táblázattal vagy az X segédfüggvénnyel lehet elvégezni. A táblázat függvényében szereplő minden mintermhez egy oszlopot rendel – a soroknak prím implikánsok felelnek meg:

 

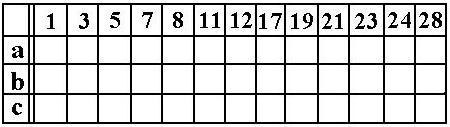
Először azokat a prím implikánsokat “vesszük fel”, melyek olyan minterm sorszámot tartalmaznak, amelyik másik prím implikánsokban nem szerepel, majd továbbiakat is. Egymás után annyi prím implikánst jelölünk be keresztekkel, amennyi ahhoz szükséges, hogy minden minterm oszlopában legalább egy kereszt legyen. A mostani példánkban ehhez mind a három prím implikánsra szükség van:



 
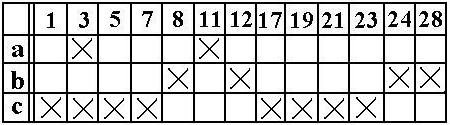
    Ha bármelyik prím implikánst elhagyjuk, azonnal lesz olyan minterm, mely már nem szerepel a függvényben, pedig a példa kiírásában szerepel. A táblázat is igazolja, hogy a példa függvényének egyszerűsített alakja:

F=a+b+c.

Az X segédfüggvény jelentése: “mely prím implikánsokra van szükség a feladat logikai függvényének legegyszerűbb kialakításához?”

Erre úgy ad választ, hogy az egyes, a feladatban szereplő minterm sorszámokhoz összegyűjtjük azokat a prím imlikánsokat, melyekben szerepelnek – ezek bármelyike az adott mintermet megvalósítja, ezért egymással VAGY kapcsolatba kerülnek. Az egyes mintermeket megvalósító VAGY kapcsolatú részleteket egymással ÉS kapcsolatba kell hozni, hiszen az összes mintermet egyidejűleg elő kell állítani.

Esetünkben az 1 sorszámú mintermhez a “c” prím implikáns kell, a 3 sorszámúhoz VAGY a “c” VAGY az “a”, az 5 sorszámúhoz a “c”. Az eddigi eredményünket így írhatjuk fel:

X= (c) ( a + c ) ( c )

Folytatva a függvényben szereplő mintermekhez a prím implikánsok felírását, a teljes X segédfüggvény ilyen lesz:

X= (c) ( a + c ) ( c ) ( c ) ( b ) ( a ) ( b ) ( c ) ( c ) ( c ) ( c ) ( b ) ( b )

A függvényben elvégezve a beszorzásokat, a szükséges prím implikáns csoport (vagy csoportok) adódnak. A függvény átalakításához idézzük fel a téma elején is említett azonosságot:

A ( A + B ) = A .

Ezt, és az A*A=A azonosságot többször alkalmazva, az X függvény jelentősen egyszerűsödik:

X = abc

Azaz a függvény megvalósításához az “a”, “b” és a “c” prím implikánsokra van szükség – az eredmény így megegyezik a táblázatos módszerrel kapott eredménnyel:

F = a + b + c

Azt tehát két különböző úton is beláttuk, hogy mindhárom prím implikánst meg kell valósítanunk. Az utolsó lépést kell még megtennünk – a prím implikánsokat vissza kell írnunk változónevekre.

Az “a” prím implikánsban ( 3,11 (8) ) két minterm szerepel, a 3 és a 11. A változók betűjeleit a Példa megadásakor felsoroltuk, F(ABCDE) formában. Írjuk át az a 3,11 (8) prím implikánst változó nevekre! Ehhez először a prím implikánsban szereplő valamelyik (fontos: bármelyik, prím implikánsban szereplő) mintermet a változó nevekkel! Most a 11-es vagy a 3-as mintermet írhatjuk fel, talán a 3-as egyszerűbb:



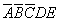
ezután a prím implikánsban szereplő összevonási számokat kettes számrendszerbeli helyiértékként értelmezve az adott helyiértéken lévő betűt kihúzzuk a felírt mintermből. A kettes számrendszerbeli helyiértékek jobbról balra nőnek:

. . . 128 64 32 16 8 4 2 1 Most, az a prím implikánsban az összevonási szám a 8, tehát ezt a helyiértéket kell kihúzni, azaz a prím implikáns: 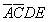   “Fordítsuk le” változónevekre a másik két prím implikánst is!

b, 8,12,24,28 (4,16) => 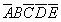 (ez a 8-as minterm), hagyjuk el a kieső helyiértékeket, így a “b” tehát: .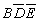

c, 1,3,5,7,17,19,21,23 (2,4,16) => 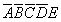 (ez az 1-es minterm, ebből kell elhagyni a 2,4 és 16 helyiértékeket): a “c” tehát .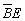

Az F függvény egyszerűsített alakja tehát:

     

                                                                

 

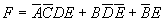
Tananyagunk végére értünk. Nincs más hátra,mint hogy kipróbáljuk mit is tanultunk meg a digitális technikából: